MULTIPLICACION DE MATRICES
Tenemos que tener en cuenta que solo puede multiplicar dos matrices si sus dimensiones son compatibles, lo que significa que el número de columnas en la primera matriz es igual al número de renglones en la segunda matriz. Si A es una matriz a × b y B es una matriz b × c , el producto AB es una matriz a × c .
La definición de la multiplicación de matrices indica una multiplicación renglón-por-columna, donde las entradas en el renglón i th de A son multiplicadas por las entradas correspondientes en el renglón j th de B y luego se suman los resultados.
La multiplicación de matrices NO es conmutativa. Si ni A ni B son una matriz identidad, AB ≠ BA.
Vamos a realizar el siguiente problema, multiplicar una matriz 2 × 3 con una matriz 3 × 2, para obtener una matriz 2 × 2 como el producto. Las entradas de la matriz producto son llamadas e ij cuando están en el renglón i th y en la columna j th .

Para obtener e 11 , multiplique el Renglón 1 de la primera matriz por la Columna 1 de la segunda.

Para obtener e 12 , multiplique el Renglón 1 de la primera matriz por la Columna 2 de la segunda.

Para obtener e 21 , multiplique el Renglón 2 de la primera matriz por la Columna 1 de la segunda.

Para obtener e 22 , multiplique el Renglón 2 de la primera matriz por la Columna 2 de la segunda.

Escribiendo la matriz producto, obtenemos:

Por lo tanto, hemos motrado que:


Lo que nos piden en este ejercicio es multiplicar las matrices que se puedan multiplicar. Para ello, el número de columnas de la primera matriz debe ser igual al número de filas de la segunda matriz.
Vamos a empezar con la matriz A que tiene 3 columnas. Esta matriz la podremos multiplicar por las matrices que tengan 3 filas. En primer lugar, la podemos multiplicar por la misma matriz A, que también tiene 3 filas.
Realizamos el producto de matrices de A.A=

Multiplicamos filas por columnas:
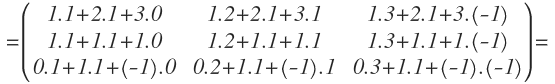
Y operamos:
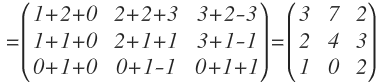
La matriz B también tiene 3 filas, por lo que podemos realizar la multiplicación de A.B=

Multiplicamos filas por columnas y operamos:

Seguimos con la matriz B que tiene 1 columna. La podemos multiplicar por cualquier matriz que tenga 1 fila, pero en este caso no tenemos ninguna, ya que la matriz A tiene 3 filas, la propia matriz B tiene 3 filas y la matriz C tiene 2 filas. Por tanto, la matriz B no la podemos multiplicar por ninguna matriz.
Por último vamos a ver los posibles productos de matrices con la matiz C. La matriz C tiene 3 columnas, por lo que la podemos multiplicar por matrices que tengan 3 filas.
La matriz A tiene 3 filas, por lo multiplicamos C.A:

Multiplicamos filas por columnas:

Y operamos:
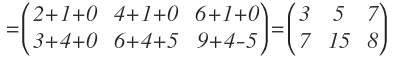
La matriz C también se puede multiplicar por la matriz B, que tiene 3 filas:

Multiplicamos filas por columnas y operamos:

EJERCICIO 2: Producto de dos matrices cuadradas de dimensión 3:
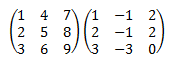
Las matrices son cuadradas la misma dimensión: .
Calculamos el producto:
![calculamos el producto de dos matrices cuadradas de dimensión 3:
[1,4,7;2,5,8;3,6,9][1,-1,2;2,-1,2;3,-3,0] =
[30, -26, 10; 36, -31, 14; 42, -36, 18] definición del producto de matrices, propiedades y
ejemplos (ejercicios resueltos)](https://www.matesfacil.com/matrices/producto3-3.png)
EJERCICIO 3: Producto de dos matrices cuadradas de dimensión 3:
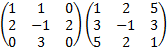
El producto es:
![calculamos el producto de dos matrices cuadradas de dimensión 3:
[1,1,0;2,-1,2;0,3,0][1,2,5;3,-1,3;5,2,1]=
[4, 1, 8; 9, 9, 9; 9, -3, 9] definición del producto de matrices, propiedades y
ejemplos (ejercicios resueltos)](https://www.matesfacil.com/matrices/producto4-3.png)
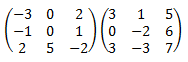
Calculamos el producto:
![calculamos el producto de dos matrices cuadradas de dimensión 3:
[-3,0,2;-1,0,1;2,5,-2][3,1,5;0,-2,6;3,-3,7]=
[-3, -9, -1; 0, -4, 2; 0, -2, 26] definición del producto de matrices, propiedades y
ejemplos (ejercicios resueltos)](https://www.matesfacil.com/matrices/producto5-3.png)
![calculamos el producto de dos matrices cuadradas de dimensión 3:
[-3,0,2;-1,0,1;2,5,-2][3,1,5;0,-2,6;3,-3,7]=
[-3, -9, -1; 0, -4, 2; 0, -2, 26] definición del producto de matrices, propiedades y
ejemplos (ejercicios resueltos)](https://www.matesfacil.com/matrices/producto5-3.png)
BIBLIOGRAFÍA:
No hay comentarios.:
Publicar un comentario